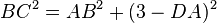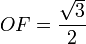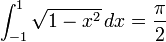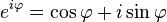Número π
π (pi) es la relación entre la longitud de una
circunferencia y su
diámetro, en
geometría euclidiana. Es un
número irracional y una de las constantes matemáticas más importantes. Se emplea frecuentemente en
matemáticas,
física e
ingeniería. El valor numérico de π,
truncado a sus primeras cifras, es el siguiente:
El nombre π
la notación con la
letra griega π proviene de la inicial de las palabras de origen
griego "
περιφέρεια" (
periferia) y "
περίμετρον" (
perímetro) de un
círculo,
[1] notación que fue utilizada primero por
William Oughtred (1574-1660), y propuesto su uso por el matemático galés
William Jones[2] (1675-1749), aunque fue el matemático
Leonhard Euler, con su obra «Introducción al cálculo infinitesimal» de
1748, quien la popularizó. Fue conocida anteriormente como
constante de Ludolph (en honor al matemático
Ludolph van Ceulen) o como
constante de Arquímedes (que no se debe confundir con el
número de Arquímedes).
Historia del cálculo del valor π
La búsqueda del mayor número de decimales del número π ha supuesto un esfuerzo constante de numerosos científicos a lo largo de la historia.
Aproximaciones geométricas a π
Es posible obtener una aproximación al valor de π de forma geométrica. De hecho, ya los griegos intentaron obtener sin éxito una solución exacta al problema del valor de π mediante el empleo de regla y compás. El problema griego conocido como cuadratura del círculo o, lo que es lo mismo, obtener un cuadrado de área igual al área de un círculo cualquiera, lleva implícito el cálculo del valor exacto de π.
Una vez demostrado que era imposible la obtención de π mediante el uso de regla y compás, se desarrollaron varios métodos aproximados. Dos de las soluciones aproximadas más elegantes son las debidas a Kochanski (usando regla y compás) y la de Mascheroni (empleando únicamente un compás).
[editar] Método de Kochanski
Se dibuja una circunferencia de radio R. Se inscribe el triángulo equilátero OEG. Se traza una recta paralela al segmento EG que pase por A, prolongándola hasta que corte al segmento OE, obteniendo D. Desde el punto D y sobre ese segmento se transporta 3 veces el radio de la circunferencia y se obtiene el punto C. El segmento BC es aproximadamente la mitad de la longitud de la circunferencia.
- Demostración (suponiendo R = 1)
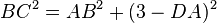
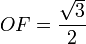

Sustituyendo en la primera fórmula:

[editar] Método de Mascheroni
Método desarrollado por Lorenzo Mascheroni: se dibuja una circunferencia de radio R y se inscribe un hexágono regular. El punto D es la intersección de dos arcos de circunferencia: BD con centro en A', y CD con centro en A. Obtenemos el punto E como intersección del arco DE, con centro en B, y la circunferencia. El segmento AE es un cuarto de la longitud de la circunferencia, aproximadamente.
- Demostración (suponiendo R = 1)




Por el teorema de Ptolomeo, en el cuadrilátero ABEB'


[editar] Uso en matemáticas y ciencia
π es ubicuo en matemática; aparece incluso en lugares que carecen de una conexión directa con los círculos de la geometría euclídea.[20]
[editar] Geometría y trigonometría
Para cualquier círculo de radio r y diámetro d = 2r, la longitud de la circunferencia es πd y el área del círculo es πr2. Además, π aparece en fórmulas para áreas y volúmenes de muchas otras figuras geométricas relacionadas con la circunferencia, como elipses, esferas, conos, y toroides.[21] π aparece en integrales definidas que describen la circunferencia, área o volumen de figuras generadas por circunferencias y círculos. En el caso básico, la mitad del área de un círculo unitario es:[22]
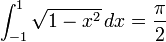
y la mitad de la longitud de la circunferencia unitaria es:[23]

Se puede integrar formas más complejas como sólidos de revolución.[24]
De la definición de las funciones trigonométricas desde el círculo unitario se llega a que el seno y el coseno tienen período 2π. Lo que significa, para todo x y enteros n, sin(x) = sin(x + 2πn) y cos(x) = cos(x + 2πn). Porque sin(0) = 0, sin(2πn) = 0 para todos los enteros n. Además, el ángulo 180° es igual a π radianes. En otras palabras 1° = (π/180) radianes.
En la matemática moderna, π es a menudo definido usando funciones trigonométricas, por ejemplo como el menor entero positivo x para el cual sinx = 0, para evitar dependencias innecesarias de las sutilezas de la geometría euclidiana y la integración. Equivalentemente, π puede ser definido usando funciones trigonométricas inversas, por ejemplo como π = 2 arccos(0) o π = 4 arctan(1). Expandir funciones trigonométricas inversas como series de potencias es la manera más fácil de obtener series infinitas para π.
[editar] Análisis superior y teoría de números
La frecuente aparición de π en análisis complejo puede estar relacionada con el comportamiento de la función exponencial de una variable compleja, descrito por la fórmula de Euler
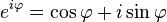
donde i es la unidad imaginaria que satisface la ecuación i2 = − 1 y e ≈ 2.71828 es el número de Euler. Esta fórmula implica que las potencias imaginarias de e describen rotaciones un círculo unitario en el plano complejo; estas rotaciones tienen un período de 360º = 2π. En particular, la rotación de 180º φ = π resulta en la notable identidad de Euler

Hay n diferentes raíces n-ésimas de la unidad

La integral de Gauss

Una consecuencia es que el resultado de la división entre la función gamma de un semientero (la mitad de un número impar) y √π es un número racional.